要解决的问题

当集合元素数量非常大时，如何判断一个元素是否存在一个集合中？

常规思路利用普通数据结构(数组、链表、树、哈希表)存储集合，再对每一个需要判断的元素进行比对。

对于元素数量非常大的集合，普通计算机无法提供如此大的内存进行存储。

布隆过滤器介绍

• 巴顿布隆于1970年提出。
• 一个很长的二进制位数组。
• 一系列哈希函数。
• 空间效率和查询效率很高。
• 有一定的误判率。

常规思路下，对于超大数据量，哈希表是空间复杂度比较好的数据结构，不需要存储元素值。可以利用哈希函数将一个元素映射到一个位数组中的一个位，如果该位不为1，则集合中肯定不存在该值。(如果该位为1，则集合中不一定存在该值)。

如何进一步降低空间占用率？使用多个哈希函数。

一个Bloom Filter是基于一个m位的位向量（b1,…bm），这些位向量的初始值为0。另外，还有一系列的hash函数（h1,…hk），这些hash函数的值域属于1~m。

对每个要查询的元素，都经过k个哈希函数映射到位向量，如果==有一个位置不为1，则该元素一定不在集合中。如果每个位置都为1，则该元素可能在集合中。==

举例

下图是一个bloom filter插入x,y,z并判断某个值w是否在该数据集的示意图：

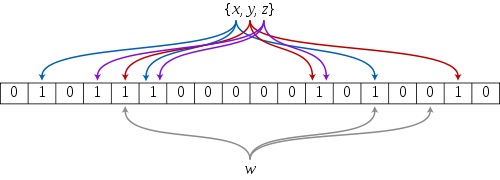
上图中，m=18，k=3；插入x是，三个hash函数分别得到蓝线对应的三个值，并将对应的位向量改为1，插入y，z时，类似的，分别将红线，紫线对应的位向量改为1。查找时，当查找x时，三个hash值对应的位向量都为1，因此判断x在此数据集中。y，z也是如此。但是查找w时，w有个hash值对应的位向量为0，因此可以判断不在此集合中。但是，假如w的最后那个hash值比上图中的大1，这是就会认为w在此集合中，而事实上，w可能不在此集合中，因此可能出现误报。显然的，插入数据越多，1的位数越多，误报的概率越大。

删除

如果使用位数组，则只支持add和isExist操作。

要支持删除可以将位数组改为计数值，增加一个值就是对应索引槽的值加一，删除就是减一。但是删除前必须确保被删除的元素之前被加入过。

特点

因为布隆过滤器能够用较少的内存占用==过滤出绝对不存在的值==，适用于过滤查询中不存在的值，减少磁盘IO或网络请求。

本文地址：https://cheng-dp.github.io/2019/03/22/bloom-filter/